Aprior源码阅读分析

Aprior源码阅读报告

Apriori算法是经典的挖掘频繁项集和关联规则的数据挖掘算法。一般而言，关联规则的挖掘是一个两步的过程：首先找出所有的频繁项集，其次由频繁项集产生强关联规则。接下来我从网上查找了一份Aprior源代码，进行阅读并写下自己的理解。

代码参考：https://www.cnblogs.com/llhthinker/p/6719779.html

首先了解Aprior算法的基本概念：
项与项集：设itemset={item1, item_2, …, item_m}是所有项的集合，其中，item_k(k=1,2,…,m)成为项。项的集合称为项集（itemset），包含k个项的项集称为k项集(k-itemset)。
事务与事务集：一个事务T是一个项集，它是itemset的一个子集，每个事务均与一个唯一标识符Tid相联系。不同的事务一起组成了事务集D，它构成了关联规则发现的事务数据库。
关联规则：关联规则是形如A=>B的蕴涵式，其中A、B均为itemset的子集且均不为空集，而A交B为空。
支持度(support)：关联规则的支持度定义如下：

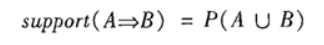
其中表示事务包含集合A和B的并（即包含A和B中的每个项）的概率。注意与P(A or B)区别，后者表示事务包含A或B的概率。

置信度(confidence)：关联规则的置信度定义如下：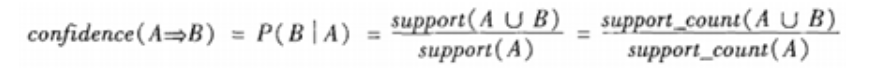

项集的出现频度(support count)：包含项集的事务数，简称为项集的频度、支持度计数或计数。
频繁项集(frequent itemset)：如果项集I的相对支持度满足事先定义好的最小支持度阈值（即I的出现频度大于相应的最小出现频度（支持度计数）阈值），则I是频繁项集。
强关联规则：满足最小支持度和最小置信度的关联规则，即待挖掘的关联规则。

python3算法代码如下：

首先定义了一个初始化数据集合函数：

def load_data_set():

    data_set = [['l1', 'l2', 'l5'], ['l2', 'l4'], ['l2', 'l3'],
            ['l1', 'l2', 'l4'], ['l1', 'l3'], ['l2', 'l3'],
            ['l1', 'l3'], ['l1', 'l2', 'l3', 'l5'], ['l1', 'l2', 'l3']]
    return data_set

每个项都是候选一项集的集合C1的成员。首先扫描所有的事务，获得每个项，生成C1。函数定义为：

def create_C1(data_set):

    C1 = set()
    for t in data_set:
        for item in t:
            item_set = frozenset([item])
            C1.add(item_set)
    return C1

由于存在先验性质：任何非频繁的(k-1)项集都不是频繁k项集的子集。因此，如果一个候选k项集Ck的(k-1)项子集不在Lk-1中，则该候选也不可能是频繁的，从而可以从Ck中删除，获得压缩后的Ck。is_apriori函数用于判断是否满足先验性质。

def is_apriori(Ck_item, Lksub1):

    for item in Ck_item:
        sub_Ck = Ck_item - frozenset([item])
        if sub_Ck not in Lksub1:
            return False
    return True

Apriori算法假定项集中的项按照字典序排序。如果Lk-1中某两个的元素（项集）itemset1和itemset2的前(k-2)个项是相同的，则称itemset1和itemset2是可连接的。所以itemset1与itemset2连接产生的结果项集是{itemset1[1], itemset1[2], …, itemset1[k-1], itemset2[k-1]}。
create_Ck函数中包含剪枝步骤，即若不满足先验性质，剪枝：

def create_Ck(Lksub1, k):

    Ck = set()
    len_Lksub1 = len(Lksub1)
    list_Lksub1 = list(Lksub1)
    for i in range(len_Lksub1):
        for j in range(1, len_Lksub1):
            l1 = list(list_Lksub1[i])
            l2 = list(list_Lksub1[j])
            l1.sort()
            l2.sort()
            if l1[0:k-2] == l2[0:k-2]:
                Ck_item = list_Lksub1[i] | list_Lksub1[j]
                # pruning
                if is_apriori(Ck_item, Lksub1):
                    Ck.add(Ck_item)
    return Ck

基于压缩后的Ck，扫描所有事务，对Ck中的每个项进行计数，然后删除不满足最小支持度的项，从而获得频繁k项集。函数定义为：

def generate_Lk_by_Ck(data_set, Ck, min_support, support_data):

    Lk = set()
    item_count = {}
    for t in data_set:
        for item in Ck:
            if item.issubset(t):
                if item not in item_count:
                    item_count[item] = 1
                else:
                    item_count[item] += 1
    t_num = float(len(data_set))
    for item in item_count:
        if (item_count[item] / t_num) >= min_support:
            Lk.add(item)
            support_data[item] = item_count[item] / t_num
    return Lk

使用数据集、最小支持度生成所有的频繁项集，函数定义为：

def generate_L(data_set, k, min_support):

    support_data = {}
    C1 = create_C1(data_set)
    L1 = generate_Lk_by_Ck(data_set, C1, min_support, support_data)
    Lksub1 = L1.copy()
    L = []
    L.append(Lksub1)
    for i in range(2, k+1):
        Ci = create_Ck(Lksub1, i)
        Li = generate_Lk_by_Ck(data_set, Ci, min_support, support_data)
        Lksub1 = Li.copy()
        L.append(Lksub1)
    return L, support_data

一旦找出了频繁项集，就可以直接由它们产生强关联规则。对于每个频繁项集itemset，产生itemset的所有非空子集（这些非空子集一定是频繁项集），对于itemset的每个非空子集s,如果，则输出，其中min_conf是最小置信度阈值。函数定义为：

def generate_big_rules(L, support_data, min_conf):

    big_rule_list = []
    sub_set_list = []
    for i in range(0, len(L)):
        for freq_set in L[i]:
            for sub_set in sub_set_list:
                if sub_set.issubset(freq_set):
                    conf = support_data[freq_set] / support_data[freq_set - sub_set]
                    big_rule = (freq_set - sub_set, sub_set, conf)
                    if conf >= min_conf and big_rule not in big_rule_list:
                        # print freq_set-sub_set, " => ", sub_set, "conf: ", conf
                        big_rule_list.append(big_rule)
            sub_set_list.append(freq_set)
    return big_rule_list

在所有函数定义完后，定义main函数，首先对Lk-1的自身连接生成的集合执行剪枝策略产生候选k项集Ck，然后，扫描所有事务，对Ck中的每个项进行计数。然后根据最小支持度从Ck中删除不满足的项，从而获得频繁k项集。获得k项集后则可以产生强关联规则：

if __name__ == "__main__":
    data_set = load_data_set()
    L, support_data = generate_L(data_set, k=3, min_support=0.2)
    big_rules_list = generate_big_rules(L, support_data, min_conf=0.7)
    for Lk in L:
        print ("="*50)
        print ("frequent " + str(len(list(Lk)[0])) + "-itemsets\t\tsupport")
        print ("="*50)
        for freq_set in Lk:
            print (freq_set, support_data[freq_set])
    print ("Big Rules")
    for item in big_rules_list:
        print(item[0], "=>", item[1], "conf: ", item[2])

==================================================
frequent 1-itemsets		support
==================================================
frozenset({'l3'}) 0.6666666666666666
frozenset({'l1'}) 0.6666666666666666
frozenset({'l4'}) 0.2222222222222222
frozenset({'l2'}) 0.7777777777777778
frozenset({'l5'}) 0.2222222222222222
==================================================
frequent 2-itemsets		support
==================================================
frozenset({'l3', 'l2'}) 0.4444444444444444
frozenset({'l1', 'l2'}) 0.4444444444444444
frozenset({'l1', 'l3'}) 0.4444444444444444
frozenset({'l5', 'l2'}) 0.2222222222222222
frozenset({'l1', 'l5'}) 0.2222222222222222
frozenset({'l2', 'l4'}) 0.2222222222222222
==================================================
frequent 3-itemsets		support
==================================================
frozenset({'l1', 'l5', 'l2'}) 0.2222222222222222
frozenset({'l1', 'l3', 'l2'}) 0.2222222222222222
Big Rules
frozenset({'l5'}) => frozenset({'l2'}) conf:  1.0
frozenset({'l5'}) => frozenset({'l1'}) conf:  1.0
frozenset({'l4'}) => frozenset({'l2'}) conf:  1.0
frozenset({'l5', 'l2'}) => frozenset({'l1'}) conf:  1.0
frozenset({'l1', 'l5'}) => frozenset({'l2'}) conf:  1.0
frozenset({'l5'}) => frozenset({'l1', 'l2'}) conf:  1.0